- Hey there! Before you dive into the full article, here is a quick and simple overview of what we are going to cover today:
- First, we'll explore displacement in cartesian coordinate.
- We will also deep dive into why do we study this? (real life examples).
- You'll learn some interesting facts about simplest definition.
- Make sure not to miss the part where we discuss key formula box.
- First, we'll explore detailed derivation (step-by-step for exams).
- We will also deep dive into step-by-step derivation.
Displacement in Cartesian Coordinate
Hello students! Today we are going to learn about displacement in Cartesian coordinate. Don't worry if it looks hard, we will make it very simple.
See, the logic is very simple. When an object moves, it changes its position. We need a proper system to track this change. That system is the Cartesian coordinate system, which uses the
Why do we study this? (Real Life Examples)
Physics is not just formulas, beta. It is about understanding the world around us. Why do we need displacement? Because we need to know the net change in position, not just the path taken.
For example, have you noticed how GPS in your mobile phone works? When you start driving from point A to point B, the road distance might be 10 km. But the displacement, which is the straight line from A to B, might only be 7 km. Engineers use the Cartesian system to calculate this shortest distance (the displacement vector) instantly, even if you are moving in three dimensions (like climbing a hill).
Another example is launching a weather rocket or a drone. Suppose a drone needs to lift off from the coordinates
Even in something simple like a billiards table (which is a 2D plane), when a ball is hit, its initial position
Simplest Definition
Definition:
Displacement (
Diagram
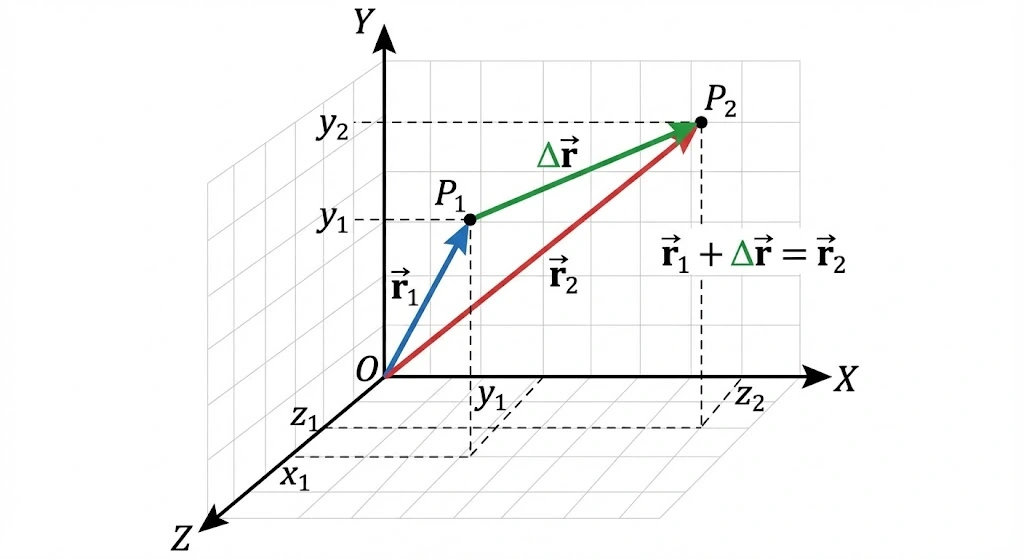
Figure: Detailed description of diagram for displacement in Cartesian coordinate
*A diagram showing a standard 3D Cartesian coordinate system (X, Y, Z axes intersecting at Origin O).
*Two points
Key Formula Box
This is the main formula, you must remember this point for exams.
Detailed Derivation (Step-by-Step for Exams)
Step-by-Step Derivation
This derivation is very important. It is often asked in 5-mark questions. We will use the concept of position vectors and the Triangle Law of Vector Addition.
Step 1: Defining Initial and Final Position Vectors
Let us consider a body moving from an initial point
The position vector for the initial point
The position vector for the final point
Here,
Step 2: Applying the Vector Law
Now, see the diagram. According to the Triangle Law of Vector Addition, the initial position vector plus the displacement vector must equal the final position vector.
Therefore, the displacement vector
Step 3: Substitution and Calculation of the Displacement Vector
Now, let us put the values of Eq. 1 and Eq. 2 into Eq. 3. Remember, we substitute the entire vector expression.
We must now group the terms based on the unit vectors
Taking the unit vectors common:
This is the required formula for the displacement vector in Cartesian coordinates.
Step 4: Finding the Magnitude of Displacement
Since displacement is a vector, we often need to find its length, or magnitude,
If a vector
Here, the components of
Therefore, the magnitude of the displacement is:
This is the magnitude of the displacement, which is the shortest distance between
Important Table
| Symbol | Meaning | Type of Quantity | Standard Unit (SI) | Remarks |
|---|---|---|---|---|
| Initial Position Vector | Vector | meter (m) | Always starts from Origin (O). | |
| Final Position Vector | Vector | meter (m) | Always starts from Origin (O). | |
| Displacement Vector | Vector | meter (m) | Change in position ( | |
| Magnitude of Displacement | Scalar | meter (m) | The length of the displacement vector. |
Solved Numericals (Exam Style)
Solved Numericals (Exam Style)
You must know how to apply these formulas. Practice these three problems well.
Q1: A particle moves in a 2D plane from point A (2 m, 3 m) to point B (8 m, 11 m). Calculate the displacement vector (
Ans:
Given:
Initial Position,
To Find: Displacement Vector
Formula:
Calculation:
- Calculate the change in
m - Calculate the change in
m - Substitute these values into the formula:
Final Answer with units:
The displacement vector is
Q2: An aeroplane moves from an initial location
Ans:
Given:
Initial Position Vector:
To Find: Magnitude of Displacement
Formula:
Calculation:
First, find the displacement vector
m Now, calculate the magnitude using the components:
m
Final Answer with units:
The magnitude of the displacement is
Q3: A bug crawls from
Ans:
Given:
To Find:
Formula:
Calculation:
Calculate the displacement vector
Calculate the magnitude
Calculate the unit vector
Final Answer with units:
Displacement vector:
Exam Corner: Questions & Answers
Short Answer Questions (2 Marks)
Q1: Distinguish clearly between Distance and Displacement.
Ans:
| Feature | Distance | Displacement |
|---|---|---|
| Definition | Total path length travelled. | Shortest straight-line change in position. |
| Nature | Scalar quantity (only magnitude). | Vector quantity (magnitude and direction). |
| Path Dependency | Depends on the path taken. | Independent of the path taken; depends only on endpoints. |
Q2: Can displacement be zero even if the distance covered is large? Give an example.
Ans:
Yes, displacement can be zero even if the distance covered is large. This happens when the initial position (
Q3: What is the physical significance of the unit vectors
Ans:
The unit vectors
Long Answer Questions (5 Marks)
Q1: Derive the complete formula for the displacement vector
Ans: (This answer requires the student to reproduce the derivation from Section 6.)
Concept: We define the movement using position vectors relative to the origin O, and then use the Triangle Law of Vector Addition to find the change in position.
1. Position Vector Definitions:
The position vector for
2. Displacement Definition:
The displacement vector
3. Substitution and Grouping:
Substituting the component forms:
We collect the coefficients of the respective unit vectors (
Q2: Starting with the displacement vector formula, derive the expression for the magnitude of displacement.
Ans:
1. Starting Formula:
We know the displacement vector
Let the components of displacement be:
2. Application of Pythagorean Theorem:
The magnitude of any vector
3. Final Substitution:
Substituting the component definitions back:
This derived expression gives the magnitude (length) of the displacement vector, which is always positive and measured in meters.
Multiple Choice Questions (MCQs)
These types of questions are common in IIT JAM and other entrance tests.
Q1: The initial position vector of a particle is
Ans: B) - Reasoning:
Q2: If a particle moves such that its displacement vector is
Ans: D) - Reasoning: Magnitude
Q3: Which statement is always true regarding distance (
Ans: C) - Reasoning: Distance must always be greater than or equal to the straight-line displacement (equality only occurs for straight-line motion without reversal).
Q4: A stone is thrown straight up and returns to the hand of the thrower. If the maximum height reached was 5 m, the net displacement of the stone is: A) 10 m B) 5 m C) -5 m D) Zero
Ans: D) - Reasoning: Initial and final positions are the same (the hand), so displacement is zero.
Q5: The position vector of a body changes from
Ans: B) - Reasoning:
Summary
So, students, we have covered the concept of displacement vector thoroughly. Remember that displacement is the change in the position vector, and it is crucial because it accounts for direction. In 3D Cartesian coordinates, we simply subtract the initial components from the final components:
I hope this concept is clear now. Practice the derivation twice, and make sure you understand how to calculate the magnitude using the Pythagorean theorem. All the best for your upcoming exams!
For more notes visit on universityscope.com .. Notes are complete for college exam and according to university