Unit Vector in Physics – Definition, Formula, Derivation and Examples

Unit Vector

Hello students! Today we are going to learn about Unit vector. Don’t worry if it looks hard, we will make it very simple.

See, vectors are essential in Physics because they tell us both how much (magnitude) and in which way (direction) something is happening. The Unit Vector is very special because it only cares about the direction. It is a mathematical tool we use to specify a direction clearly, without confusing it with the actual size or magnitude of the physical quantity.

Why do we study this? (Real Life Examples)

Now, why is this topic important for us? You must always ask: Where do I see this in real life? The study of the Unit vector is fundamental because direction matters in everything we do.

1. Satellite Dish Positioning: Have you seen the small dish antenna on your roof? It must be pointed exactly towards the satellite in space. The magnitude (the size of the dish) is fixed, but if the direction changes by even a tiny bit, you lose the signal. The exact pointing direction is defined using a unit vector.
2. The Ceiling Fan: When the fan is rotating, the axis of rotation is defined by a vector. We might ask, “Is the fan rotating clockwise or counter-clockwise?” To specify this rotation’s direction (using the right-hand rule), we use a unit vector along the axis. The actual speed (magnitude) is separate from the axis direction.
3. GPS Navigation: When you use Google Maps, it tells you to move $5$ kilometers, but more importantly, it says “move East” or “move North-East.” The direction part—East, West, etc.—is essentially a unit vector telling you the precise bearing you need to take.

Simplest Definition

Definition: A Unit vector is a vector that has a magnitude (or length) of exactly one (unity) and is used solely to indicate the direction of a given vector.

The Unit vector of any vector $\mathbf{A}$ is denoted by $\hat{A}$ (read as ‘A-cap’ or ‘A-hat’).

Diagram

`

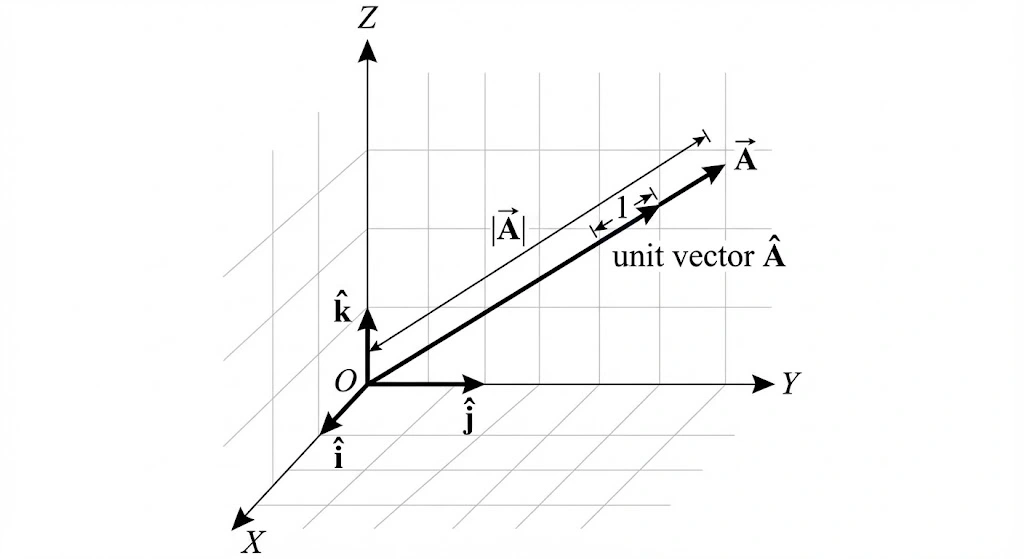
Figure: A line segment representing the vector A ($\mathbf{A}$) starting from the origin. The total length is marked as $|\mathbf{A}|$. A small segment of length 1, pointing in the same direction as $\mathbf{A}$, is marked as the unit vector $\hat{A}$. The axes X, Y, Z should be labeled, and the corresponding standard unit vectors $\hat{i},\hat{j},\hat{k}$ should be shown pointing along the respective axes.

`

Key Formula Box

This formula is very important. You must remember this for numerical problems.

Here, $\hat{A}$ is the Unit vector, $\mathbf{A}$ is the original vector, and $|\mathbf{A}|$ is the magnitude of the original vector.

Detailed Derivation (Step-by-Step for Exams)

Step-by-Step Derivation

This derivation is often asked in 5-mark questions. Pay attention to every step.

Step 1: Defining the General Vector

See, the logic is very simple. Any vector, let’s call it $\mathbf{A}$, can always be written as a product of two things:

1. Its actual length or size (Magnitude).
2. The direction in which it points (Unit vector).

So, mathematically, we write this fundamental relationship:

$$\mathbf{A}=(\text{Magnitude of }\mathbf{A})\times (\text{Unit Vector in the direction of }\mathbf{A})$$

We use the standard symbols: $$\mathbf{A}=|\mathbf{A}|\cdot \hat{A}\text{— (1)}$$

Step 2: Isolating the Unit Vector

Our goal is to find the expression for the Unit vector $\hat{A}$. We need to rearrange Equation (1).

We want to keep $\hat{A}$ on one side (usually the RHS). So, we must move the magnitude term, $|\mathbf{A}|$, to the other side (LHS).

Since $|\mathbf{A}|$ is multiplying $\hat{A}$ on the RHS, when we move it to the LHS, it goes into the denominator (it divides the term already present there).

$$\hat{A}=\frac{\mathbf{A}}{|\mathbf{A}|}\text{— (2)}$$

This is the main formula for the Unit Vector.

Step 3: Expression in Cartesian Coordinates

Now, let us make this more practical for calculations. Suppose our vector $\mathbf{A}$ is given in the standard Cartesian system ($x,y,z$). We know that the unit vectors along the axes are $\hat{i}$, $\hat{j}$, and $\hat{k}$ respectively.

The vector $\mathbf{A}$ can be written using its components $(A_x,A_y,A_z)$:

$$\mathbf{A}=A_x\hat{i}+A_y\hat{j}+A_z\hat{k}\text{— (3)}$$

Step 4: Calculating the Magnitude

To use Equation (2), we need the magnitude $|\mathbf{A}|$. By using the Pythagorean theorem in three dimensions, the magnitude is given by:

$$|\mathbf{A}|=\sqrt{A_x^2+A_y^2+A_z^2}\text{— (4)}$$

Step 5: Final Comprehensive Expression

Finally, we substitute the expressions for $\mathbf{A}$ (from Eq 3) and $|\mathbf{A}|$ (from Eq 4) back into our main formula for the unit vector (Eq 2).

$$\hat{A}=\frac{\mathbf{A}}{|\mathbf{A}|}$$

$$\hat{A}=\frac{A_x\hat{i}+A_y\hat{j}+A_z\hat{k}}{\sqrt{A_x^2+A_y^2+A_z^2}}$$

This complete expression is the one you will use for all exam calculations. You must write this final step clearly.

Important Table

Standard Unit Vectors in Cartesian Coordinates:

Solved Numericals (Exam Style)

You must practice these types of problems. They usually come for 3 marks.

Q1: Find the unit vector in the direction of $\mathbf{P}=3\hat{i}+4\hat{j}$.

Ans: Given: Vector $\mathbf{P}=3\hat{i}+4\hat{j}$ To Find: Unit vector $\hat{P}$. Formula: $$\hat{P}=\frac{\mathbf{P}}{|\mathbf{P}|}$$

Calculation: Step 1: Calculate the magnitude $|\mathbf{P}|$. $$|\mathbf{P}|=\sqrt{P_x^2+P_y^2}$$ $$|\mathbf{P}|=\sqrt{(3{)}^2+(4{)}^2}$$ $$|\mathbf{P}|=\sqrt{9+16}$$ $$|\mathbf{P}|=\sqrt{25}$$ $$|\mathbf{P}|=5$$

Step 2: Substitute magnitude and vector into the formula. $$\hat{P}=\frac{3\hat{i}+4\hat{j}}{5}$$

Step 3: Simplify (This is good practice for the final answer). $$\hat{P}=\frac{3}{5}\hat{i}+\frac{4}{5}\hat{j}$$

Final Answer with units: The unit vector is $\hat{P}=0.6\hat{i}+0.8\hat{j}$. (Unit vectors are dimensionless.)

Q2: A vector $\mathbf{Q}$ has a magnitude of 10 units and is directed parallel to the vector $\mathbf{A}=6\hat{i}-8\hat{j}$. Determine the expression for vector $\mathbf{Q}$.

Ans: Given: Magnitude of $\mathbf{Q}$, $|\mathbf{Q}|=10$. $\mathbf{Q}$ is parallel to $\mathbf{A}=6\hat{i}-8\hat{j}$. To Find: Vector $\mathbf{Q}$. Formula: $$\mathbf{Q}=|\mathbf{Q}|\cdot \hat{A}$$ (Since $\mathbf{Q}$ is parallel to $\mathbf{A}$, the direction of $\mathbf{Q}$ is the unit vector $\hat{A}$.)

Calculation: Step 1: Find the unit vector $\hat{A}$ first. First, calculate the magnitude of $\mathbf{A}$: $$|\mathbf{A}|=\sqrt{(6{)}^2+(-8{)}^2}$$ $$|\mathbf{A}|=\sqrt{36+64}$$ $$|\mathbf{A}|=\sqrt{100}$$ $$|\mathbf{A}|=10$$

Now, find the unit vector $\hat{A}$: $$\hat{A}=\frac{\mathbf{A}}{|\mathbf{A}|}=\frac{6\hat{i}-8\hat{j}}{10}$$ $$\hat{A}=0.6\hat{i}-0.8\hat{j}$$

Step 2: Calculate the vector $\mathbf{Q}$. $$\mathbf{Q}=|\mathbf{Q}|\cdot \hat{A}$$ $$\mathbf{Q}=10\cdot (0.6\hat{i}-0.8\hat{j})$$ $$\mathbf{Q}=(10\times 0.6)\hat{i}-(10\times 0.8)\hat{j}$$ $$\mathbf{Q}=6\hat{i}-8\hat{j}$$

Final Answer with units: The vector is $\mathbf{Q}=6\hat{i}-8\hat{j}$ units.

Q3: Given two vectors $\mathbf{A}=\hat{i}-2\hat{j}+3\hat{k}$ and $\mathbf{B}=2\hat{i}+\hat{j}-\hat{k}$. Find the unit vector parallel to the resultant vector $\mathbf{R}=\mathbf{A}+\mathbf{B}$.

Ans: Given: $\mathbf{A}=\hat{i}-2\hat{j}+3\hat{k}$ and $\mathbf{B}=2\hat{i}+\hat{j}-\hat{k}$. To Find: Unit vector $\hat{R}$. Formula: $\hat{R}=\frac{\mathbf{R}}{|\mathbf{R}|}$

Calculation: Step 1: Calculate the resultant vector $\mathbf{R}$. $$\mathbf{R}=\mathbf{A}+\mathbf{B}$$ $$\mathbf{R}=(\hat{i}-2\hat{j}+3\hat{k})+(2\hat{i}+\hat{j}-\hat{k})$$ Now, combine the components (i with i, j with j, k with k): $$\mathbf{R}=(1+2)\hat{i}+(-2+1)\hat{j}+(3-1)\hat{k}$$ $$\mathbf{R}=3\hat{i}-1\hat{j}+2\hat{k}$$

Step 2: Calculate the magnitude of the resultant $|\mathbf{R}|$. $$|\mathbf{R}|=\sqrt{(3{)}^2+(-1{)}^2+(2{)}^2}$$ $$|\mathbf{R}|=\sqrt{9+1+4}$$ $$|\mathbf{R}|=\sqrt{14}$$

Step 3: Find the unit vector $\hat{R}$. $$\hat{R}=\frac{\mathbf{R}}{|\mathbf{R}|}$$ $$\hat{R}=\frac{3\hat{i}-\hat{j}+2\hat{k}}{\sqrt{14}}$$

Final Answer with units: The unit vector parallel to the resultant is $\hat{R}=\frac{1}{\sqrt{14}}(3\hat{i}-\hat{j}+2\hat{k})$.

Exam Corner: Questions & Answers

Short Answer Questions (2 Marks Each)

Q: State two main properties of a Unit Vector.

Ans:

1. Magnitude is Unity: The magnitude (or modulus) of any unit vector is always exactly equal to one ($|\hat{A}|=1$).
2. Direction Specification: Its sole purpose is to indicate the precise direction of the original vector in space. It is a dimensionless quantity, meaning it does not carry units.

Q: What is the significance of the expression $\hat{A}\cdot \hat{B}=0$?

Ans: The expression $\hat{A}\cdot \hat{B}=0$ is the dot product of two unit vectors. We know the dot product formula is $AB\cos \theta$. Since $\hat{A}$ and $\hat{B}$ are unit vectors, their magnitudes $A$ and $B$ are both 1. So, $1\cdot 1\cdot \cos \theta =0$. This means $\cos \theta =0$. Therefore, the angle $\theta$ between the two unit vectors must be ${90}^{\circ }$ ($\pi /2$ radians). This signifies that the two unit vectors $\hat{A}$ and $\hat{B}$ are perpendicular (orthogonal) to each other.

Q: Express the direction cosines of a vector $\mathbf{A}$ using its unit vector $\hat{A}$.

Ans: Let the vector be $\mathbf{A}=A_x\hat{i}+A_y\hat{j}+A_z\hat{k}$. The unit vector is: $$\hat{A}=\frac{A_x}{|\mathbf{A}|}\hat{i}+\frac{A_y}{|\mathbf{A}|}\hat{j}+\frac{A_z}{|\mathbf{A}|}\hat{k}$$ The direction cosines $(l,m,n)$ are defined as the cosine of the angles the vector makes with the x, y, and z axes, respectively. $$l=\cos \alpha =\frac{A_x}{|\mathbf{A}|}$$ $$m=\cos \beta =\frac{A_y}{|\mathbf{A}|}$$ $$n=\cos \gamma =\frac{A_z}{|\mathbf{A}|}$$ Thus, the unit vector is simply: $$\hat{A}=l\hat{i}+m\hat{j}+n\hat{k}$$

Long Answer Questions (5 Marks Each)

Q: Define Unit Vector. Derive the complete expression for the unit vector $\hat{A}$ in terms of its components $A_x,A_y,A_z$. (The derivation must be complete.)

Ans: Definition: A Unit vector is a vector whose magnitude is one (unity) and which is used purely to indicate the direction of a vector quantity. It is denoted by a cap ($\hat{A}$).

Complete Derivation:

Step 1: Basic Vector Relationship A vector $\mathbf{A}$ can always be written as the product of its magnitude and its unit vector: $$\mathbf{A}=|\mathbf{A}|\cdot \hat{A}\text{(1)}$$

Step 2: Unit Vector Formula Rearranging Eq (1) to isolate the unit vector: $$\hat{A}=\frac{\mathbf{A}}{|\mathbf{A}|}\text{(2)}$$

Step 3: Component Representation of Vector $\mathbf{A}$ If $\mathbf{A}$ is expressed in terms of its components along the Cartesian axes ($\hat{i},\hat{j},\hat{k}$): $$\mathbf{A}=A_x\hat{i}+A_y\hat{j}+A_z\hat{k}\text{(3)}$$

Step 4: Calculation of Magnitude $|\mathbf{A}|$ The magnitude of $\mathbf{A}$ is calculated using the distance formula (Pythagorean theorem in 3D): $$|\mathbf{A}|=\sqrt{A_x^2+A_y^2+A_z^2}\text{(4)}$$

Step 5: Final Unit Vector Expression Substitute the full expressions for $\mathbf{A}$ (Eq 3) and $|\mathbf{A}|$ (Eq 4) back into the main unit vector formula (Eq 2).

$$\hat{A}=\frac{A_x\hat{i}+A_y\hat{j}+A_z\hat{k}}{\sqrt{A_x^2+A_y^2+A_z^2}}$$

This expression successfully defines the unit vector purely in terms of the components of the original vector.

Multiple Choice Questions (MCQs)

Q1: The magnitude of any unit vector is always: A) Dependent on the coordinate system B) Zero C) Infinity D) One

Ans: D) – The definition of a unit vector is that its magnitude is unity (one).

Q2: If $\mathbf{B}=12\hat{i}-5\hat{k}$, what is the magnitude of the unit vector $\hat{B}$? A) 13 B) 1 C) $\sqrt{169}$ D) $\sqrt{17}$

Ans: B) – The magnitude of any unit vector, regardless of the components of the original vector, is always 1.

Q3: The unit vector along the negative z-axis is represented by: A) $\hat{k}$ B) $-\hat{k}$ C) $\hat{j}$ D) $-\hat{i}$

Ans: B) – The standard unit vector along the positive z-axis is $\hat{k}$. The opposite direction is therefore $-\hat{k}$.

Q4: A vector $\mathbf{P}$ is such that $\mathbf{P}=5\hat{P}$. What is the magnitude of $\mathbf{P}$? A) 1 B) 5 C) 0 D) Cannot be determined

Ans: B) – Since $\hat{P}$ is the unit vector (magnitude 1), the equation $\mathbf{P}=5\times (1)$ means the magnitude of $\mathbf{P}$ is 5.

Q5: If $\hat{A}=0.5\hat{i}+0.5\hat{j}+n\hat{k}$ is a unit vector, the value of $n$ must be: A) 1 B) $\frac{1}{\sqrt{2}}$ C) $\sqrt{0.5}$ D) $\sqrt{2}$

Ans: C) – For $\hat{A}$ to be a unit vector, $|\hat{A}{|}^2=1$. $$(0.5{)}^2+(0.5{)}^2+n^2=1$$ $$0.25+0.25+n^2=1$$ $$0.50+n^2=1$$ $$n^2=1-0.5=0.5$$ $$n=\sqrt{0.5}$$

Summary

So, students, I hope this concept of the Unit vector is clear now. Remember, the Unit vector is like the compass that tells us where to go, separate from how far we have to travel. Its single most important property is that its magnitude is always one. Practice the derivation twice, and make sure you show all steps when calculating the magnitude for numerical problems. This topic is fundamental for understanding mechanics and electromagnetism later on! All the best!